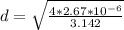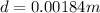Question

cylindrical water tank is 20.0 m tall, open to the atmosphere at the top, and is filled to the top. It is noticed that a small hole has occurred in the side at a point 16.5 m below the water level and that water is flowing out at the volume flow rate of 2.90 10-3 m3/min. Determine the following. (a) the speed in m/s at which water is ejected from the hole

Answer 1

a

The velocity is
`v =17.98 \ m/s`

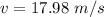
b

The diameter is
`d = 0.00184m`

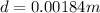
Step-by-step explanation:

The diagram of the set up is shown on the first uploaded image

From the question we are told that

The height of the water tank is
`h = 20.0 \ m`

The position of the hole
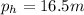`p_h = 16.5m` below water level

The rate of water flow
`\r V = 2.90 *10^(-3) m^3 /min = (2.90 *10^(-3))/(60) = 0.048*10^(-3) m^3/s`

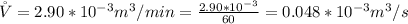
According to Bernoulli's theorem position of the hole

`(P_o + h \rho g)/(\rho) + (1)/(2) u^2 = (P_o)/(\rho ) + (1)/(2) v^2`

Where u is the initial speed the water through the hole = 0 m/s

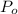`P_o` is the atmospheric pressure

`(P_o )/(\rho) + ( h \rho g)/(\rho) + 0 = (P_o)/(\rho ) + (1)/(2) v^2`

`v = √(2gh)`

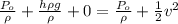
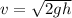
Substituting value

`v = √(2 * 9.8 * 16.5 )`

`v =17.98 \ m/s`

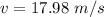
The Volumetric flow rate is mathematically represented as

`\r V = A * v`

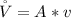
Making A the subject

`A = (\r V)/(v)`

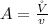
substituting value

`A = (0.048 *10^(-3))/(17.98)`

`= 2.66*10^(-6)m^2`

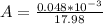
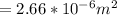
Area is mathematically represented as

`A = (\pi d^2)/(4)`

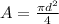
making d the subject

`d = \sqrt{(4*A)/(\pi) }`

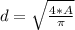
Substituting values

`d = \sqrt{(4 * 2.67 *10^(-6))/(3.142) }`

`d = 0.00184m`