Question

Safety regulations state that roller coasters cannot operate safely in high winds. Throughout the day, ride operators measure the wind speed at several random locations along the track to verify that the speed is below an established threshold value, allowing the ride to operate safely. The collected data is used to conduct a one-sample z -test of the null hypothesis that the mean wind speed is moderate against the alternative that the mean wind speed is too high. If the null hypothesis is rejected in favor of the alternative, the ride is shut down due to unsafe conditions. Choose the correct description of a type I error and a type II error in this context.

Answer 1

Type I error would be to conclude that the mean wind speed is too high and decide to shut down the ride but in actual the wind speed was moderate and it is safe to do riding.

Type II error would be to conclude that the mean wind speed is moderate and decide to go on riding but in actual the wind speed is too high and it unsafe to go on riding and should be shut down.

Explanation:

We are given that the collected data is used to conduct a one-sample z -test of the null hypothesis that the mean wind speed is moderate against the alternative that the mean wind speed is too high.

If the null hypothesis is rejected in favor of the alternative, the ride is shut down due to unsafe conditions.

So, Null Hypothesis,
`H_0` : The mean wind speed is moderate.

Alternate Hypothesis,
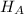`H_A` : The mean wind speed is too high.

Also, it is provided that if the null hypothesis is rejected in favor of the alternative, the ride is shut down due to unsafe conditions.

• Now, Type I error states the Probability of rejecting null hypothesis given the fact that it was true or Probability of rejecting the true hypothesis.

So, in the given context, Type I error would be to conclude that the mean wind speed is too high and decide to shut down the ride but in actual the wind speed was moderate and it is safe to do riding.

• On the other hand, Type II error states the Probability of accepting null hypothesis given the fact that it was false or Probability of accepting the false hypothesis.

So, in the given context, Type II error would be to conclude that the mean wind speed is moderate and decide to go on riding but in actual the wind speed is too high and it unsafe to go on riding and should be shut down.