Answer:
![\vec{E}=\vec{E_1}+\vec{E_2}=[25856\hat{i}+163443.2\hat{j}]N/C](https://img.qammunity.org/2021/formulas/mathematics/college/bd96403n705tiulowvbc4vnccct54h02b5.png)
Explanation:
The electric field is given by:
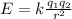
k: Coulomb's constant = 8.98*10^9 Nm^2/C^2
at the point P(0,0.5m) you have both x ad y component of the electric field. For the particle q1 you have:
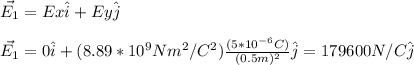
for the particle q2, it is necessary to compute the angle between the E vector and the axis, by using the distance y and x. Furthermore it is necessary to know the distance from q2 to the point P.
![\vec{E_2}=Excos\theta \hat{i}-Eysin\theta \hat{j}\\\\\theta=tan^(-1)((0.5)/(0.8))=32\°\\\\r=√(0.5^2+0.8^2)=0.94m\\\\\vec{E_2}=(8.89*10^9Nm^2/C^2)((-3*10^(-6C)))/((0.94m)^2)[cos(32)\hat{i}-sin(32)\hat{j}]\\\\=[25856.06\hat{i}-16156.71\hat{j}]N/C](https://img.qammunity.org/2021/formulas/mathematics/college/pw952r34rdadnjb4lil6srar4sl5j6vjpd.png)
Finally, by adding E1 and E2 you obtain:
![\vec{E}=\vec{E_1}+\vec{E_2}=[25856\hat{i}+163443.2\hat{j}]N/C](https://img.qammunity.org/2021/formulas/mathematics/college/bd96403n705tiulowvbc4vnccct54h02b5.png)