Question

A disease has hit a city. The percentage of the population infected t days after the disease arrives is approximated by ​p(t)equals7 t e Superscript negative t divided by 8 for 0less than or equalstless than or equals32. After how many days is the percentage of infected people a​ maximum? What is the maximum percent of the population​ infected?

Answer 1

(1) The percentage of infected people will be a​ maximum after 8 days.

(2) The maximum percent of the population​ infected is 20.60%.

Explanation:

The percentage of the population infected t days after the disease arrives is approximated by:

`p(t)=7te^(-t/8);\ 0\leq t\leq 32`

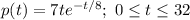
(1)

The percentage of infected people will be a​ maximum when p' (t) = 0.

Compute the value of p' (t) and equate it to 0 as follows:

`p '(t) = 7(1)e^(-t/8) +7te^(-t/8)(-1/8)`

`0=e^(-t/8)(7 -(7t)/(8))\\`

`0=7-(7t)/(8)\\0=56-7t\\7t=56\\t=8`

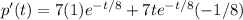
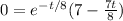
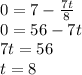
Thus, the percentage of infected people will be a​ maximum after 8 days.

(2)

Compute the value of p (8) as follows:

`p(8)=7*8* e^(-8/8)\\=7* 8* 0.36788\\=20.60128\\\approx 20.60\%`

Thus, the maximum percent of the population​ infected is 20.60%.