Answer:
The dimensions for the rectangle are 'x'= 50ft and 'y'= 50ft
The maximum area for the goats = 2500ft^2
Explanation:
Step(l):-
Given a farmer has 200 feet to fence to enclose a regular area for goats
Given perimeter of the rectangle
2(x + y) = 200
x + y = 100
y = 100 -x …(l)
Step(ll):-
The Area of the rectangle = length × breadth
A = x y
A = x (100 -x)
A = 100x - x² …(ii)
Differentiating equation (ii) with respective to 'x' we get
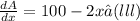
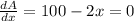
100 -2x =0
100 = 2x
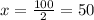
Step(lll):-
Again differentiating equation (lll) with respective to 'x' , we get
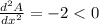
The maximum value at x = 50
y = 100 - x
y = 100 - 50 =50
The dimensions are x = 50 and y = 50
The Area of the rectangle = 50×50 = 2500ft^2
Conclusion:-
The dimensions for the rectangle
length of the rectangle 'x'= 50ft and
width of the rectangle 'y'= 50ft
The maximum area for the goats = 2500ft^2