Question

A farmer has 200 feet to fence to

enclose a regular area for goats. What

dimensions for the rectangle will maximize the area for the goats?

Answer 1

The dimensions for the rectangle are 'x'= 50ft and 'y'= 50ft

The maximum area for the goats = 2500ft^2

Explanation:

Step(l):-

Given a farmer has 200 feet to fence to enclose a regular area for goats

Given perimeter of the rectangle

2(x + y) = 200

x + y = 100

y = 100 -x …(l)

Step(ll):-

The Area of the rectangle = length × breadth

A = x y

A = x (100 -x)

A = 100x - x² …(ii)

Differentiating equation (ii) with respective to 'x' we get

`(dA)/(dx) = 100 -2x …(lll)`

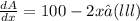
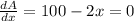
`(dA)/(dx) = 100 -2x =0`

100 -2x =0

100 = 2x

`x = (100)/(2) = 50`

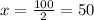
Step(lll):-

Again differentiating equation (lll) with respective to 'x' , we get

`(d^(2) A)/(dx^(2) ) = -2 < 0`

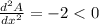
The maximum value at x = 50

y = 100 - x

y = 100 - 50 =50

The dimensions are x = 50 and y = 50

The Area of the rectangle = 50×50 = 2500ft^2

Conclusion:-

The dimensions for the rectangle

length of the rectangle 'x'= 50ft and

width of the rectangle 'y'= 50ft

The maximum area for the goats = 2500ft^2