Question

A garden hose with an internal diameter of 2.9 cm is connected to a (stationary) lawn sprinkler that consists merely of a container with 24 holes, each 0.36 cm in diameter. If the water in the hose has a speed of 0.98 m/s, at what speed does it leave the sprinkler holes?

Answer 1

Water leaves the holes with a speed of 2.65 m/sec

Step-by-step explanation:

It is given internal diameter of garden hose = 2.9 cm

So internal radius
`r_1=(2.9)/(2)=1.45cm`

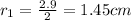
Number of holes n = 24

Diameter of holes d = 0.36 cm

So radius of holes
`r_2=(0.36)/(2)=0.18cm`

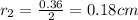
Velocity of water in hose
`v_1=0.98m/sec`

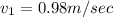
According to continuity equation

`A_1v_1=nA_2v_2`

`\pi r_1^2* 0.98=24* \pi r_2^2* * v_2`

`1.45^2* 0.98=24* 0.18^2* * v_2`

`v_2=2.65m/sec`

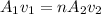
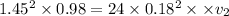
Therefore water leaves the holes with a speed of 2.65 m/sec