Answer:
The instantaneous axis of rotation=
x = 0 ; z = 8.4 ft
Step-by-step explanation:
Given:
Speed of helicopter, Vo= 120 mi/h, converting to ft/sec, we have:
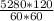
= 176 ft/s
Angular velociyy, w = 220 rpm, converting to rad/sec, we have:
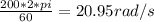
The helicopter moves horizontally in the x direction at a speed of 120 mi/h, this means that the helicopter moves in the positive x direction at 120mi/h
To find the instantaneous axis of rotation of the main blades, we have:
Where Vc = 20.95 rad/s
Vo = 176 ft/s

= 8.4 ft
Therefore the axis of rotation=
x = 0 ; z = 8.4 ft