Finding the coefficient a of the term in the expansion of the binomial.(x^(2) + 3)^(12) ax^(8)

Question

Finding the coefficient a of the term in the expansion of the binomial.
`(x^(2) + 3)^(12) ax^(8)`

Answer 1

3,247,695

Explanation:

We want the coefficient of the term with x^8

So Use Newton's Binomial Expansion formula

Formula is (x + y) ^n = Sum for i=0 to n (n choose i) x^(n-i)*y^i

here (x^2 + 3) ^ 12

( 12 choose i) * (x^2)^(12-i) * (3)^i

i needs to equal 8 for us to get x^8

(12 choose 8) * (x^2)^(12-8) * (3^8)

= (12 choose 8) * x^8 * (3^8)

so a = (12 choose 8) *
`3^(8)`

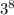
a = (12! /(8! * 4!) ) *
`3^(8)`

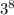
a = ( 12*11*10*9/ 4*3*2*1) *
`3^(8)`

a = (11*5*9) *
`3^(8)`

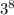
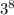
a = 11*5*9 * 6561

a = 3,247,695