Answer:
(a) The test statistic value is, 5.382.
(b) Retain the null hypothesis.
Explanation:
A Chi-square test for goodness of fit will be used in this case.
The hypothesis can be defined as:
H₀: The observed frequencies are same as the expected frequencies.
Hₐ: The observed frequencies are not same as the expected frequencies.
The test statistic is given as follows:
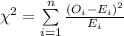
The information provided is:
Observed values:
Half Pint: 36
XXX: 35
Dark Night: 9
TOTAL: 80
The expected proportions are:
Half Pint: 40%
XXX: 40%
Dark Night: 20%
Compute the expected values as follows:
E (Half Pint)
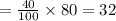
E (XXX)
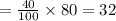
E (Dark night)

Compute the test statistic as follows:
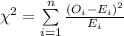
![=[((36-32)^(2))/(32)]+[((35-32)^(2))/(32)]+[((9-16)^(2))/(16)]](https://img.qammunity.org/2021/formulas/mathematics/college/mknjy3tnqywzyl788ynuvrn6jzigjk2wpf.png)
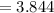
The test statistic value is, 5.382.
The degrees of freedom of the test is:
n - 1 = 3 - 1 = 2
The significance level is, α = 0.05.
Compute the p-value of the test as follows:
p-value = 0.1463
*Use a Ch-square table.
p-value = 0.1463 > α = 0.05.
So, the null hypothesis will not be rejected at 5% significance level.
Thus, concluding that the production of the premium lagers matches these consumer preferences.