Question

Suppose a manufacturer makes two types of skis: a trick ski and a slalom ski. Each trick ski requires 8 hours of design work and 4 hours of finishing. Each slalom ski requires 8 hours of design and 12 hours of finishing. Furthermore, the total number of hours allocated for design work is 160 and the total available for finishing work is 180. Finally, the number of tricks skis produced must be less than or equal to 15. How many trick and slalom skis can be made under these conditions? The profit on each trick ski is $5 and the profit on each slalom ski is $10.

Answer 1

The company can make 13 trick skis and 6 slalome skis

Step-by-step explanation:

For trick skis:

8 hours design

4 hours finishing

For Slalom skis:

8 hours design

12 hours finishing

Total number for design = 160

Total number for finishing= 180

Therefore we have:

8x + 8y = 160

4x + 12y = 180

Let's solve with substitution method

8x + 8y = 160........*1

4x + 12y = 180........*2

We now have:

8x + 8y = 160

8x + 24y = 360

= -32y = -200

`y = (200)/(32)`

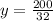
y = 6.25

Let's substitute 6.25 for y in equation 1.

8x + 8(6.25) = 160

= 8x = 160 - 50

`x = (110)/(8)`

x = 13.75

x = 13.75 and y = 6.25

The company can make a 13 trick skis and 6 slalom skis.