Question

At the moment a hot cake is put in a cooler, the difference between the cake's and the cooler's temperatures is 50° Celsius. This causes the cake to cool and the temperature difference loses (1/5) of it's value every minute.

Write a function that gives the temperature difference in degrees Celsius, D(t), t minutes after the cake was put in the cooler.

Answer 1

See answer below

Explanation:

Hi there,

The prompt is trying to showcase exponential functions, and specifically exponential decay, where over the course of the independent variable (time in this example) the dependent variable (temp difference) exponentially drops.

To start, when a math prompt says something like "at the moment xyz begins" it usually means time zero. Thus, we have 1 point already, the y-intercept:

`D(0)= 50 \ C`°

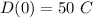Now, we notice that it says it "loses 1/5 of its original value every minute" which is code for exp. decay. So, to account for this, the remaining value is just b = 1 - 0.2 = 0.8.

Exponential Decay formula:

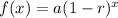`f(x) = a (1-r)^x` where a is a constant, and constant r
`< 1`

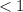
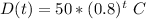`D(t) = 50 * (0.8)^t \ C`° where t is in minutes

thanks,

Answer 2

Answer:: D(t)= 50(4/5)^t

Step-by-step explanation: If 1/5 of the temperature difference is lost each minute, that means 4/5 of the difference remains each minute. So each minute, the temperature difference is multiplied by a factor of 4/5 (or 0.8).

If we start with the initial temperature difference, 50° Celsius, and keep multiplying by 4/5, this function gives us the temperature difference t minutes after the cake was put in the cooler.