Answer:
(a)Length =2 feet
(b)Width =2 feet
(c)Height=3 feet
Explanation:
Let the dimensions of the box be x, y and z
The rectangular box has a square base.
Therefore, Volume of the box
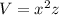
Volume of the box

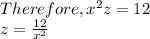
The material for the base costs
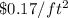 , the material for the sides costs
, the material for the sides costs
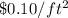 , and the material for the top costs
, and the material for the top costs
 .
.
Area of the base
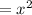
Cost of the Base

Area of the sides
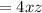
Cost of the sides=
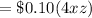
Area of the Top
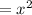
Cost of the Base

Total Cost,
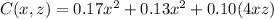
Substituting
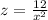
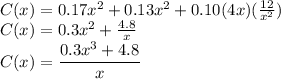
To minimize C(x), we solve for the derivative and obtain its critical point
![C'(x)=(0.6x^3-4.8)/(x^2)\\Setting \:C'(x)=0\\0.6x^3-4.8=0\\0.6x^3=4.8\\x^3=4.8/ 0.6\\x^3=8\\x=\sqrt[3]{8}=2](https://img.qammunity.org/2021/formulas/mathematics/college/xypbbaenncy2esgxkktq2ydur9sfvynbly.png)
Recall:
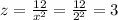
Therefore, the dimensions that minimizes the cost of the box are:
(a)Length =2 feet
(b)Width =2 feet
(c)Height=3 feet