Answer:
112.76°
Step-by-step explanation:
The angle of the reflected light is the same as the angle of the incident light:
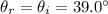
The refracted angle is obtained by using the Snell's law:
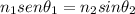
n1: air index of refraction ≈ 1.00
n2: ice index of refraction = 1.31
By replacing the values for the incident angle and the index of refraction you can calculate the angle of refraction:

the angle between the reflected and refracted angle will be:
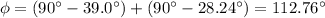
where you have taken into account that the angles aremeasured according to the horizontal axis.