Question

A rocket is launched from a tower. The height of the rocket, y in feet, is related to the time after launch, x in seconds, by the given equation. Using this equation, find the time that the rocket will hit the ground, to the nearest 100th of second.

EQUATION:

y=-16x^2+281x+137

Answer 1

It will take 18.04s for the rocket to hit the ground.

Explanation:

Solving a quadratic equation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

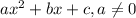This polynomial has roots
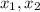`x_(1), x_(2)` such that
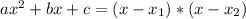`ax^(2) + bx + c = (x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\bigtriangleup))/(2*a)`

`x_(2) = (-b - √(\bigtriangleup))/(2*a)`

`\bigtriangleup = b^(2) - 4ac`

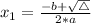
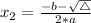
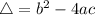
In this problem:

Height given by the following equation:

`y = -16x^(2) + 281x + 137`

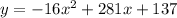
It hits the ground when y = 0. So

`-16x^(2) + 281x + 137 = 0`

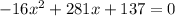
Multiplying by -1

`16x^(2) - 281x - 137 = 0`

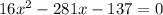
So
`a = 16, b = -281, c = -137`

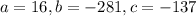
Then

`\bigtriangleup = (-281)^(2) - 4*16*(-137) = 87729`

`t_(1) = (-(-281) + √(87729))/(2*16) = 18.04`

`t_(2) = (-(-281) - √(87729))/(2*16) = -0.4747`

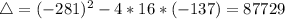
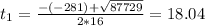
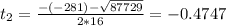
It cannot take negative time, so we discard
`t_(2)`

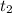
It will take 18.04s for the rocket to hit the ground.