Answer:
![D(t) = 1\,m + (0.2\,m)\cdot \sin \left[\right(2\,(rad)/(s) \left)\cdot t\right]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/4iqss4fr5ac1hihiq0fkj36babir6iois9.png)
Explanation:
The sinusoidal expression has the following form:

Where:
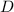 - Initial distance from the floor of the lake, in meters.
- Initial distance from the floor of the lake, in meters.
 - Amplitude of oscillation, in meters.
- Amplitude of oscillation, in meters.
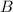 - Angular frequency, in radians.
- Angular frequency, in radians.
Now, each coefficient is derived as follows:
Initial distance from the floor of the lake

Amplitude of oscillation
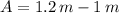
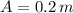
Angular frequency
From the statement it is known that boat reaches its maximum height in a quarter of its oscillation. Then, the angular frequency is:
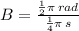
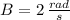
The expression is:
![D(t) = 1\,m + (0.2\,m)\cdot \sin \left[\right(2\,(rad)/(s) \left)\cdot t\right]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/4iqss4fr5ac1hihiq0fkj36babir6iois9.png)