Question

Which statements about functions g(x) = x2 - 4x + 3 and f(x) = x2 - 4x are true? Select all that apply.

A. The vertex of the graph of function g is above the vertex of the graph of function f.
B. The graphs have the same axis of symmetry.
c. Function f has a maximum value and function g has a minimum value.​

Answer 1

The answer is B!

Explanation:

Plato answer

Answer 2

A and B

Explanation:

We are given that

`g(x)=x^2-4x+3`

`g(x)=(x^2-2* x* 2+4)-4+3=(x-2)^2-1`

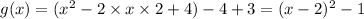
Compare with it

`y=(x-h)^2+k`

Where vertex=(h,k)

We get

Vertex of g=(2,-1)

`f(x)=x^2-4x=(x^2-2* x* 2+4)-4=(x-2)^2-4`

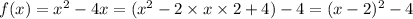
Vertex of f=(2,-4)

Equation of axis of symmetry=x-coordinate of vertex

Axis of symmetry of g

x=2

Axis of symmetry of f

x=2

Differentiate w.r.t x

`g'(x)=2x-4=0`

`2x-4=0\implies 2x=4`

`x=(4)/(2)=2`

`f'(x)=2x-4`

`2x-4=0\implies 2x=4`

`x=(4)/(2)=2`

`g''(x)=2>0`

`f''(x)=2>0`

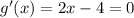
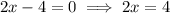
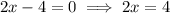
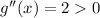
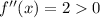
f and g have both minima at x=2

Hence, option A and B are true.