Answer:
The coefficient of variation for A is 24.6%.
The coefficient of variation for B is 33.7%.
Explanation:
The coefficient of variation (CV) is well defined as the ratio of the standard deviation to the mean. It exhibits the degree of variation in association to the mean of the population.
The formula to compute the coefficient of variation is,
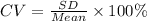
Consider the data set A.
Compute the mean of the data set A as follows:
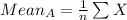
![=(1)/(14)* [36900+19400+...+26000+38400]\\=30064.2857](https://img.qammunity.org/2021/formulas/mathematics/college/yryzvb0ovlzj66795419pgzbnu3gdebt1w.png)
Compute the standard deviation of the data set A as follows:
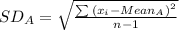

Compute the coefficient of variation for A as follows:
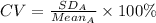
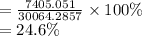
The coefficient of variation for A is 24.6%.
Consider the data set B.
Compute the mean of the data set B as follows:
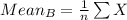
![=(1)/(11)* [2.1+5.0+...+4.1+1.7]\\=3.2455](https://img.qammunity.org/2021/formulas/mathematics/college/38oeeotvowvrtjuwksh8fpgtwrvzepa7tt.png)
Compute the standard deviation of the data set B as follows:
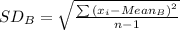
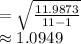
Compute the coefficient of variation for B as follows:
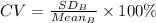
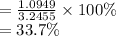
The coefficient of variation for B is 33.7%.