Answer:
The number of different combinations of 3 books that Erika can take on a trip if she has 5 books is 10
Explanation:
Here we have the formula for combination given as follows;
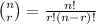
Where n is the number of set elements = 5 and
r = Number of subset elements = 3
Therefore, plugging the values, we have;
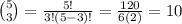
Therefore, the number of different combinations of 3 books that Erika can take on a trip if she has 5 books = 10.