Question

According to ​Lambert's law​, the intensity of light from a single source on a flat surface at point P is given by Upper L equals k cosine squared (theta )where k is a constant. ​(a) Write L in terms of the sine function. ​(b) Why does the maximum value of L occur when thetaequals​0?

Answer 1

(a)
`L = k*(1 - sin^(2)(\theta))`

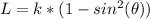
(b) L reaches its maximum value when θ = 0 because cos²(0) = 1

Explanation:

Lambert's Law is given by:

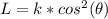`L = k*cos^(2)(\theta)` (1)

(a) We can rewrite the above equation in terms of sine function using the following trigonometric identity:

`cos^(2)(\theta) + sin^(2)(\theta) = 1`

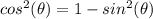`cos^(2)(\theta) = 1 - sin^(2)(\theta)` (2)

By entering equation (2) into equation (1) we have the equation in terms of the sine function:

`L = k*(1 - sin^(2)(\theta))`

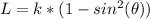
(b) When θ = 0, we have:

`L = k*cos^(2)(\theta) = k*cos^(2)(0) = k`

We know that cos(θ) is a trigonometric function, between 1 and -1 and reaches its maximun values at nπ, when n = 0,1,2,3...

Hence, L reaches its maximum value when θ = 0 because cos²(0) = 1.

I hope it helps you!

Answer 2

`(a)L=k(1-sin^2\theta)\\(b)\text{0 is a critical point of L}`

Explanation:

According to ​Lambert's law​, the intensity of light from a single source on a flat surface at point P is given by:

`L=kcos^2\theta, $ k is a constant\\`

(a)We are required to write L in terms of the sine function.

`cos^\theta+sin^2\theta=1\\cos^\theta=1-sin^2\theta\\L=k(1-sin^2\theta)\\`

(b)To obtain the maximum value of the function L, we examine its critical points.

`L=k-ksin^2\theta\\L'=2sin\theta cos\theta\\L'=sin 2\theta\\sin 2\theta=0\\2\theta=arcSin0\\2\theta=0\\\theta=0`

The maximum value of L occur when
`\theta=0` because 0 is a critical point of the function L.