Question

In the past, 60% of all undergraduate students enrolled at a State University in NY earned their degrees within four years of matriculation. Administrators want to test the claim made by some faculty memebers that this proportion has fallen below the historical value of 60%. A random sample of 95 students from the class that matriculated in the fall of 2012 was recently selected to test this hypothesis. Administrators found that 44 of these 95 students graduated in the spring of 2016 (i.e., four academic years after matriculation). Use a significance level of 5%. Formulate the hypotheses. What is the value of the test statistic? What is the critical value of the test? Find the p-value of the test. What is your conclusion? Explain it in the context of the problem.How do you do this in excel?

Answer 1

The null and alternative hypothesis are:

`H_0: \pi=0.6\\\\H_a:\pi<0.6`

The value of the test statistic is z=-2.617.

The critical value for a one-tailed test with significance level α=0.05 is zc=--1.645.

The P-value is P=0.0044.

To calculate this P-value in excel, we use the function NORM.S.DIST(-2.617;TRUE).

Explanation:

This is a hypothesis test for a proportion.

The claim is that the proportion of undergraduate students enrolled at a State University in NY earned their degrees within four years of matriculation has fallen below 60%.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.6\\\\H_a:\pi<0.6`

The significance level is 0.05.

The sample has a size n=95.

The sample proportion is p=0.4632.

`p=X/n=44/95=0.4632`

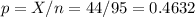
The standard error of the proportion is:

`\sigma_p=\sqrt{(\pi(1-\pi))/(n)}=\sqrt{(0.6*0.4)/(95)}\\\\\\ \sigma_p=√(0.00253)=0.0503`

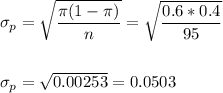
Then, we can calculate the z-statistic as:

`z=(p-\pi-0.5/n)/(\sigma_p)=(0.4632-0.6+0.5/95)/(0.0503)=(-0.1315)/(0.0503)=-2.617`

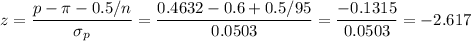
This test is a left-tailed test, so the P-value for this test is calculated as:

`P-value=P(z<-2.617)=0.0044`

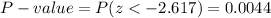
As the P-value (0.0044) is smaller than the significance level (0.05), the effect is significant.

The null hypothesis is rejected.

There is enough evidence to support the claim that the proportion of undergraduate students enrolled at a State University in NY earned their degrees within four years of matriculation has fallen below 60%.

The critical value for a one-tailed test with significance level α=0.05 is zc=--1.645.

To calculate this P-value in excel, we use the function NORM.S.DIST(-2.617;TRUE).