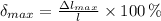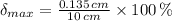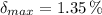Answer:
a)
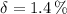 , b)
, b)
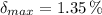
Explanation:
a) The area formula for a square is:
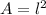
The total differential for the area is:
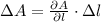
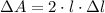
The absolute error for the area of the square is:
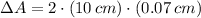
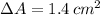
Thus, the relative error is:
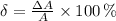
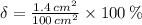
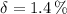
b) The maximum allowable absolute error for the area of the square is:
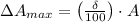
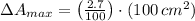
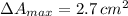
The maximum allowable absolute error for the length of a side of the square is:
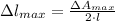
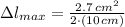
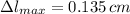
Lastly, the maximum allowable relative error is: