Answer:
The values of T which satisfies the inequality are:
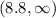
Explanation:
In the equation
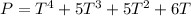
- Represent P by 10,000
- Write an inequality where the expression is greater than 10000:
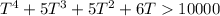
- Get 0 on one side of the inequality.
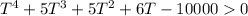
- Graph the polynomial function.
- We have real x-intercepts of 8.84 and -11.38.
- Determine intervals where the graph is above the x-axis.
- Since negative values of x in this situation are irrelevant, the values of T which satisfies the inequality are:
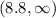
- We now test a value from the set of solution to see if it is valid.
- Let T=9

Since 10665 is grater than 10000, the result is reasonable.