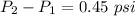Answer:
Step-by-step explanation:
By using Bernoulli's Equation:
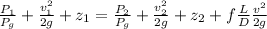
where;
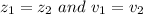


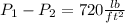
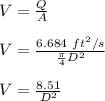
Density of gasoline
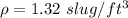
Dynamic Viscosity
 =
=

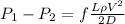
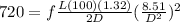
D = 1.46 f
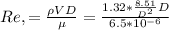
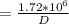
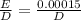
However; the trail and error is as follows;
Assume ; f= 0.02 → D = 0.667ft
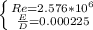
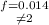
f = 0.0145 → D = 0.0428 ft
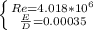

f = 0.0156 → D = 0.43 ft
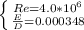
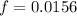
∴ pipe diameter d = 0.43 ft
Given that:
D = 1 ft
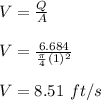
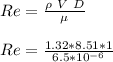
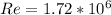
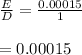
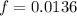
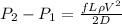
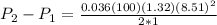
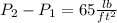 to psi ; we have:
to psi ; we have: