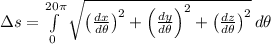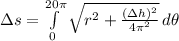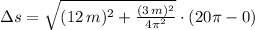Question

An architect was asked to build a special staircase in a new building. The staircase will be built like a helix that rotates around the outside of a cylindrical waterfall. Because it is a helix, the beginning of the staircase begins at a point directly above the position where the staircase ends at the bottom base of the column. Describe how to find the length of the staircase if the cylinder it surrounds is 30 m in height and has a radius of 12 m

Answer 1

`\Delta s \approx 754.579\,m` (See explanation below).

Explanation:

Each floor has a height of 3 meters. Then, the number of floors of the cylinder is:

`n = (30\,m)/(3\,m)`

`n = 10\,floors`

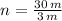
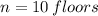
Let consider that spiral makes a revolution per floor. Then, the parametric equations of the spiral are:

`x = r\cdot \cos \theta`

`y = r\cdot \sin \theta`

`z = \Delta h \cdot (\theta)/(2\pi)`

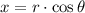
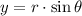
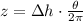
Length of the staircase can be modelled by using the formula for arc length:

`\Delta s = \int\limits^(20\pi)_(0) {\sqrt{\left((dx)/(d\theta) \right) ^(2)+\left((dy)/(d\theta) \right)^(2)+\left((dz)/(d\theta)\right)^(2)}} \, d\theta`

`\Delta s = \int\limits^(20\pi)_(0) {\sqrt{\left(-r\cdot \sin \theta\right)^(2)+\left(r\cdot \cos \theta\right)^(2)+\left((\Delta h)/(2\pi) \right)^(2)} } \, d\theta`

`\Delta s = \int\limits^(20\pi)_(0) {\sqrt{r^(2)+((\Delta h)^(2))/(4\pi^(2)) }} \, d\theta`

`\Delta s = \sqrt{(12\,m)^(2)+((3\,m)^(2))/(4\pi^(2)) } \cdot (20\pi-0)`

`\Delta s \approx 754.579\,m`