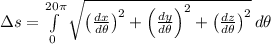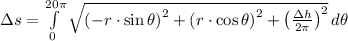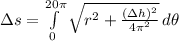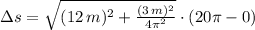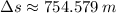Answer:
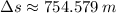 (See explanation below).
(See explanation below).
Explanation:
Each floor has a height of 3 meters. Then, the number of floors of the cylinder is:
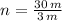
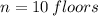
Let consider that spiral makes a revolution per floor. Then, the parametric equations of the spiral are:
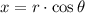
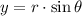
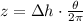
Length of the staircase can be modelled by using the formula for arc length: