Answer:
Tamara should expect the sum of the two cubes to be equal to 5 20 times.
Explanation:
The sample space of rolling a number cube are:
S = {1, 2, 3, 4, 5, 6}
If two such cubes are rolled together, then the sum of the two cubes will be 5 for the combinations below:
S₁ = {(1, 4), (2, 3), (3, 2) and (4, 1)}
The total number of outcomes will be, N = 36.
Compute the probability that the sum of rolling two numbered cubes as follows:
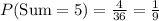
Let X = number of time the sum of the two numbers on two cubes is 5.
Two numbered cubes are rolled n = 180 times.
The event of getting a sum of 5 in independent of the other results.
The random variable X follows a Binomial distribution with parameters n = 180 and p =
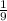 .
.
The expected value of X is:
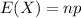
Compute the expected number of times Tamara expects the sum of the two cubes to be equal to 5 as follow:
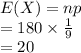
Thus, Tamara should expect the sum of the two cubes to be equal to 5 20 times.