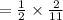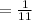Answer:
The probability that he selects a raisin bagel and then a plain bagel is
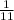 .
.
Explanation:
Probability:
The ratio of the number of outcomes of favorable event to total number of all possible outcomes is called probability of the favorable event.
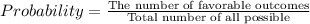
Given that, there are 4 blueberry, 6 raisins and 2 plain bangles in a bag.
Total number of bangles= (4+6+2)
= 12
The probability that he selects a raisin

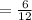
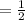
Total number of remaining bagels is =(12-1)=11
After selecting a raisin bagel,the probability that he selects a plain bangle is
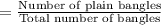
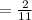
Selecting of a raisin bangle and a plain bangle are both independent event.
The probability that he selects a raisin bagel and then a plain bagel is