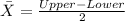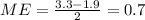Question

Use the confidence interval to find the estimated margin of error. Then find the sample mean. A biologist reports a confidence interval of left parenthesis 1.9 comma 3.3 right parenthesis when estimating the mean height​ (in centimeters) of a sample of seedlings. The estimated margin of error is nothing . The sample mean is nothing .

Answer 1

`\bar X = (Lower +Upper)/(2)`

`\bar X= (1.9+3.3)/(2)= 2.6`

And the margin of error with this one:

`\bar X = (Upper-Lower)/(2)`

`ME = (3.3-1.9)/(2)= 0.7`

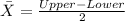
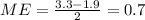
Explanation:

Assuming that the parameter of interest is the sample mean
`\mu`. And we can estimate this parameter with a confidence interval given by this formula:

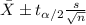`\bar X \pm t_(\alpha/2)(s)/(√(n))` (1)

For this case the confidence interval is given by (1.9, 3.3)

Since the confidence interval is symmetrical we can estimate the sample mean with this formula:

`\bar X = (Lower +Upper)/(2)`

`\bar X= (1.9+3.3)/(2)= 2.6`

And the margin of error with this one:

`\bar X = (Upper-Lower)/(2)`

`ME = (3.3-1.9)/(2)= 0.7`