Question

Is it possible to produce a continuous and oriented aramid fiber-epoxy matrix composite having longitudinal and transverse moduli of elasticity of 35 GPa and 5.17 GPa, respectively? Assume that the modulus of elasticity of the epoxy is 3.4 GPa and modulus of elasticity for aramid fibers is 131 GPa.

Answer 1

Both value of V are different, therefore, what is proposed in the question is not possible

Step-by-step explanation:

Given data:

E₁=35 GPa (longitudinal moduli of elasticity)

E₂=5.17 GPa (transverse moduli of elasticity)

Ee=3.4 GPa (elastic modulus epoxi)

Ef=131 GPa (elastic modulus fiber)

To produce a continuous and oriented aramid fiber-epoxy matrix, the volume fraction of the fibers must be the same. Then, we must calculate the volume fraction of the fibers in the longitudinal and transverse:

For the longitudinal:

`E_(1) =E_(e) (1-V)+E_(f) V\\35=3.4*(1-V)+131V`

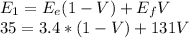
Solving for V:

V=0.2476

For the transverse:

`E_(2) =(E_(e)E_(f) )/(E_(f)*(1-V)+E_(e)V ) \\5.17=(3.4*131)/(131*(1-V)+3.4V)`

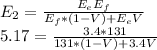
Solving for V:

V=0.3515

You can see that both value of V are different, therefore, what is proposed in the question is not possible