Answer:
a.
![\vec{u}=(\bigtriangledown F(-3,3))/(|\bigtriangledown F(-3,3)|)=(1)/(√(2))[\hat{i}-\hat{j}]](https://img.qammunity.org/2021/formulas/mathematics/college/mk8geujmg2cxcw4rz1nnmz4uyfeulo3paj.png) (ascent)
(ascent)
![\vec{u}=-(\bigtriangledown F(-3,3))/(|\bigtriangledown F(-3,3)|)=-(1)/(√(2))[\hat{i}-\hat{j}]](https://img.qammunity.org/2021/formulas/mathematics/college/bauzzmgr1xzqyacmzp52j7w5cw3mm350ph.png) (descent)
(descent)
b.
![\vec{v}=(1)/(√(2))[\hat{i}+\hat{j}]](https://img.qammunity.org/2021/formulas/mathematics/college/qow3r595gvssezm6nx1ve48766vy394t2o.png)
Explanation:
a. The function is given by:
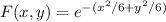
the point is P(-3,3)
a. The unit vector that gives the direction of the steepest ascent is necessary to compute the gradient of F(x,y):
![\bigtriangledown F(x,y)=e^(-(x^2/6+y^2/6))(-(x)/(3))\hat{i}+e^(-(x^2/6+y^2/6))(-(y)/(3))\hat{j}\\\\\bigtriangledown F(x,y)=-(1)/(3)e^(-(x^2/6+y^2/6))[x\hat{i}+y\hat{j}]](https://img.qammunity.org/2021/formulas/mathematics/college/g8kfwelo7fs0s7yyip7vwc9x5u64rly5uh.png)
The, it is necessary to evaluate in the point P, and to compute the norm of the vector in order to get the unit vector:
![\bigtriangledown F(-3,3)=-(1)/(3)e^{-((9)/(6)+(9)/(6))}[-3\hat{i}+3\hat{j}]\\\\\bigtriangledown F(-3,3)=e^(-3)[\hat{i}-\hat{j}]\\\\|\bigtriangledown F(-3,3)|=\sqrt{(e^(-3))^2+(e^(-3))^2}=√(2)e^(-3)\\\\\vec{u}=(\bigtriangledown F(-3,3))/(|\bigtriangledown F(-3,3)|)=(1)/(√(2))[\hat{i}-\hat{j}]](https://img.qammunity.org/2021/formulas/mathematics/college/6m4mfwssg7gfqpq6rg8rxn0hfv5w5hff09.png) (ascent)
(ascent)
for the steepest descend you have
![\vec{u}=-(\bigtriangledown F(-3,3))/(|\bigtriangledown F(-3,3)|)=-(1)/(√(2))[\hat{i}-\hat{j}]](https://img.qammunity.org/2021/formulas/mathematics/college/bauzzmgr1xzqyacmzp52j7w5cw3mm350ph.png)
b.
the vector with the direction of no change is a vector perpendicular to grad(F):
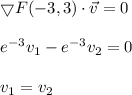
furthermore, v is an unit vector:

then, the vector is:
![\vec{v}=(1)/(√(2))[\hat{i}+\hat{j}]](https://img.qammunity.org/2021/formulas/mathematics/college/qow3r595gvssezm6nx1ve48766vy394t2o.png)