Question

Element X decays radioactively with a half life of 9 minutes. If there are 960 grams of Element X, how long, to the nearest tenth of a minute, would it take the element to decay to 40 grams?

y=a(.5)^t/h


​

Answer 1

It will take 41.3 minutes for the element to decay to 40 grams

Explanation:

The amount of element after t minute is given by the following equation:

`x(t) = x(0)e^(-rt)`

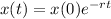
In which x(0) is the initial amount and r is the rate that it decreases.

Element X decays radioactively with a half life of 9 minutes.

This means that
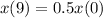`x(9) = 0.5x(0)`. We use this to find r. So

`x(t) = x(0)e^(-rt)`

`0.5x(0) = x(0)e^(-9r)`

`e^(-9r) = 0.5`

`\ln{e^(-9r)} = ln(0.5)`

`-9r = ln(0.5)`

`9r = -ln(0.5)`

`r = -(ln(0.5))/(9)`

`r = 0.077`

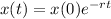
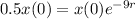
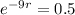
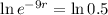
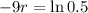
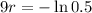
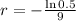
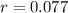
So

`x(t) = x(0)e^(-0.077t)`

There are 960 grams of Element X

This means that
`x(0) = 960`

`x(t) = 960e^(-0.077t)`

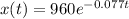
How long, to the nearest tenth of a minute, would it take the element to decay to 40 grams?

This is t when
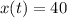`x(t) = 40`. So

`x(t) = 960e^(-0.077t)`

`40 = 960e^(-0.077t)`

`e^(-0.077t) = (40)/(960)`

`\ln{e^(-0.077t)} = \ln{(40)/(960)}`

`-0.077t = \ln{(40)/(960)}`

`0.077t = -\ln{(40)/(960)}`

`t = -\frac{\ln{(40)/(960)}}{0.077}`

`t = 41.3`

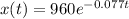
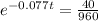
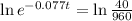
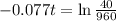
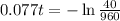
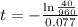
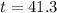
It will take 41.3 minutes for the element to decay to 40 grams