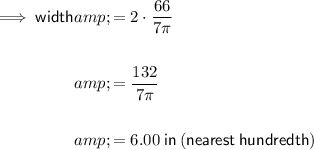Answer:
6.00 in (nearest hundredth)
Explanation:
Lateral surface area = surface area excluding the bases(s)
Lateral surface area of a cone =
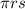
(where r is the radius and s is the slant height)
Given:
- lateral surface area ≈ 66 in²
- slant height (s) = 7 in
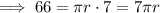
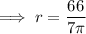
The width of the hat is the diameter. As diameter = 2r: