Question

Engineers must consider the breadths of male heads when designing helmets. The company researchers have determined that the population of potential clientele have head breadths that are normally distributed with a mean of 6.1-in and a standard deviation of 1-in. Due to financial constraints, the helmets will be designed to fit all men except those with head breadths that are in the smallest 4.3% or largest 4.3%.

Answer 1

The minimum head breadth that will fit the clientele is 4.4 inches.

The maximum head breadth that will fit the clientele is 7.8 inches.

Explanation:

Let X = head breadths of men that is considered for the helmets.

The random variable X is normally distributed with mean, μ = 6.1 and standard deviation, σ = 1.

To compute the probability of a normal distribution we first need to convert the raw scores to z-scores using the formula:

`z=(x-\mu)/(\sigma)`

It is provided that the helmets will be designed to fit all men except those with head breadths that are in the smallest 4.3% or largest 4.3%.

Compute the minimum head breadth that will fit the clientele as follows:

P (X < x) = 0.043

⇒ P (Z < z) = 0.043

The value of z for this probability is:

z = -1.717

*Use a z-table.

Compute the value of x as follows:

`z=(x-\mu)/(\sigma)\\-1.717=(x-6.1)/(1)\\x=6.1-(1.717* 1)\\x=4.383\\x\approx4.4`

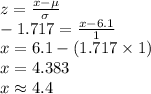
Thus, the minimum head breadth that will fit the clientele is 4.4 inches.

Compute the maximum head breadth that will fit the clientele as follows:

P (X > x) = 0.043

⇒ P (Z > z) = 0.043

⇒ P (Z < z) = 1 - 0.043

⇒ P (Z < z) = 0.957

The value of z for this probability is:

z = 1.717

*Use a z-table.

Compute the value of x as follows:

`z=(x-\mu)/(\sigma)\\1.717=(x-6.1)/(1)\\x=6.1+(1.717* 1)\\x=7.817\\x\approx7.8`

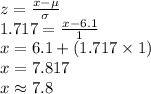
Thus, the maximum head breadth that will fit the clientele is 7.8 inches.