Answer:
B
Step-by-step explanation:
Let's convert these written languages into mathematical expressions:
"x is the average of m and 9": x =
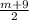
"y is the average of 2m and 15": y =
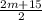
"z is the average of 3m and 18": z =
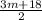
Now, we want to find the value of the average of x, y, and z in terms of m. The average of x, y, and z can be written as:
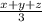 . Let's substitute each of the expressions we have above in for x, y, and z:
. Let's substitute each of the expressions we have above in for x, y, and z:
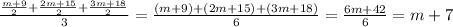
The answer is B.
Hope this helps!