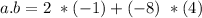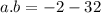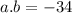Question

Find a b if a =(2,- 8) and b =(-1,4).

а. -30

b. {1,- 4}

с. -34

d. -2.- 32

Please select the best answer from the choices provided

Answer 1

`a.b = -34`

Explanation:

Given

a = (2,-8)

b = (-1,4)

Required

Product of a and b

Product of a and b can be represented as ab and this can be solved using dot product of a and b

The dot product is the sum of the products of the corresponding entries where the entries are (2,-8) and (-1,4)

Provided that a and b are vectors,

`a.b = a_1b_1+a_2b_2`

Where

`a_1 = 2, b_1 = -1, a_2 = -8, b_2 = 4`

By Substitution

`a.b = a_1b_1+a_2b_2` becomes

`a.b = 2 \ * (-1) + (-8)\ * (4)`

`a.b = (-2) + (-32)`

`a.b = -2 -32`

`a.b = -34`

Answer 2

d. -2, - 32

Explanation:

Given that,

a =(2,- 8) and b =(-1,4).

: a b = ( 2 × - 1) , ( -8 × 4)

= - 1, -32