Question

When current flows through a wire of length L and cross-sectional area A, the resistance in the wire

(choose one):

a. Is proportional to L and A

b. Is inversely proportional to L and A

6. Is proportional to L and inversely proportional to A

7. Is inversely proportional to L and proportional to A

Answer 1

Is proportional to L and inversely proportional to A

Step-by-step explanation:

The electrical resistance 'R' of a simple conductor is a function of its length and area. It is shown by the simple mathematical relation as R = pL/ A

Where,' L' is the length of the

conductor, 'A' is the cross sectional area and 'p' is the resistivity.

Answer 2

(6) Is proportional to L and inversely proportional to A.

Step-by-step explanation:

I will explain it mathematically, following formula relates Resistance to length of wire L and cross sectional area A.

`R = p(L)/(A)`

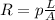
here, p is greek letter 'Rho' is called resistivity of the wire and L is lenght and A is cross sectional area of the wire.

By inspection we can tell that as length increases the resistance of wire increase, so resistance must be directly propoetional to length.

and resistance decrease as cross sectional area A decreases.

So the resistance must be directly proportional to Length of wire and inversly proportional to cross sectional area of wire.

option number (6) fits all of our deductions.