Answer:
(6) Is proportional to L and inversely proportional to A.
Step-by-step explanation:
I will explain it mathematically, following formula relates Resistance to length of wire L and cross sectional area A.
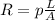
here, p is greek letter 'Rho' is called resistivity of the wire and L is lenght and A is cross sectional area of the wire.
By inspection we can tell that as length increases the resistance of wire increase, so resistance must be directly propoetional to length.
and resistance decrease as cross sectional area A decreases.
So the resistance must be directly proportional to Length of wire and inversly proportional to cross sectional area of wire.
option number (6) fits all of our deductions.