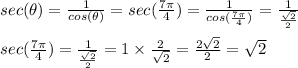Answer:

Explanation:
Just adjusting the question, since tan (0)=0 and we have a description of a trigonometric interval:
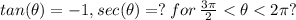
Therefore, let's go for the secant of

1). Well, firstly this interval:
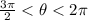 is the IV quadrant, where the tangent assumes negative values.
is the IV quadrant, where the tangent assumes negative values.
2) One of the notable arcs we have is the
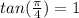
3) Then If we subtract 360º-45º=315º or
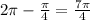 rad
rad
So this is the arc we want
So we have
In Radians:
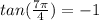
In degrees:

4) Finally, rationalizing radicals on the denominator: