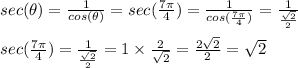Question

Given that tan 0=-1, what is the value of sec 0, for 3pi/2 < 0 < 2pi?

Answer 1

`√(2)`

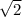
Explanation:

Just adjusting the question, since tan (0)=0 and we have a description of a trigonometric interval:

`tan (\theta)=-1, sec(\theta)=?\:for \:(3\pi)/(2) < \theta < 2\pi?`

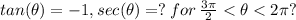
Therefore, let's go for the secant of
`\theta`

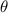
1). Well, firstly this interval:
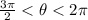`(3\pi)/(2) < \theta < 2\pi` is the IV quadrant, where the tangent assumes negative values.

2) One of the notable arcs we have is the

`tan((\pi)/(4))=1`

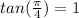
3) Then If we subtract 360º-45º=315º or
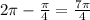`2\pi -(\pi)/(4)=(7\pi)/(4)` rad

So this is the arc we want

So we have

In Radians:

`tan ((7\pi)/(4))= -1 \\`

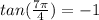
In degrees:

`tan(315\º)=-1`

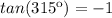
4) Finally, rationalizing radicals on the denominator:

`sec(\theta)=(1)/(cos(\theta))=sec((7\pi)/(4))=(1)/(cos((7\pi)/(4)))=(1)/((√(2))/(2))\\\\sec((7\pi)/(4))=(1)/((√(2))/(2))=1* (2)/(√(2))=(2√(2))/(2)=√(2)`

Answer 2

√2

Explanation:

Given tanθ = -1

θ = arctan(-1)

θ = -45°

Since tan θ is negative in the 2nd and 4th quadrant,

New angles:

θ = 90-45 = 45°(2nd quadrant)

θ = 360-45 = 315° (4the quadrant)

To get secθ between 3π/2< θ<2π

In trigonometry identity,

secθ = 1/cosθ

We will use θ = 315° since it is the only angle that falls within the given range

Sec315° = 1/cos315°

Sec315° = 1/(1/√2)

Sec 315° = √2