Question

In 195019501950, the per capita gross domestic product (GDP) of Australia was approximately \$1800$1800dollar sign, 1800. Each year afterwards, the per capita GDP increased by approximately 6.7\%6.7%6, point, 7, percent. Write a function that gives the approximate per capita GDP G(t)G(t)G, left parenthesis, t, right parenthesis of Australia ttt years after 195019501950.

Answer 1

1800(1+0.067)^t

Explanation:

I did it on Khan and it was right.

Answer 2

The function of capita GDP is given by

`G(t)= 1800(1+0.067)^t`

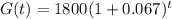
where G(t) is in dollar and t is years after 1950.

Explanation:

Given that,

in 1950, the per capita GDP of Australia was $1800.

The capita GDP is increased by 6.7 % per year.

In 1951, the capita GDP was increased =6.7% of $1800

The capita GDP was= $1800+ 6.7% of $1800

=$1800(1+6.7%)

In 1952, the capita GDP was increased =$1800(1+6.7%)

The capita GDP was=$1800(1+6.7%)+ 6.7% of$1800(1+6.7%)

=$1800(1+6.7%)(1+6.7)

= $1800(1+6.7%)²

=$1800(1+0.067)²

In 1952, the capita GDP was increased =$1800(1+6.7%)²

The capita GDP was=$1800(1+6.7%)²+ 6.7% of$1800(1+6.7%)²

=$1800(1+6.7%)²(1+6.7)

= $1800(1+6.7%)³

=$1800(1+0.067)³

and so on.

The function of capita GDP is given by

`G(t)= 1800(1+0.067)^t`

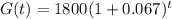
where G(t) is in dollar and t is years after 1950.