Question

In your own words, explain the Normal Distribution and provide a real world example.

Answer 1

The Normal distribution is a continuous probability distribution with possible values all the reals. Some properties of this distribution are:

Is symmetrical and bell shaped no matter the parameters used. Usually if X is a random variable normally distributed we write this like that:

`X \sim N(\mu , \sigma)`

The two parameters are:

`\mu` who represent the mean and is on the center of the distribution

`\sigma` who represent the standard deviation

One particular case is the normal standard distribution denoted by:

`Z \sim N(0,1)`

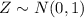
Example: Usually this distribution is used to model almost all the practical things in the life one of the examples is when we can model the scores of a test. Usually the distribution for this variable is normally distributed and we can find quantiles and probabilities associated

Explanation:

The Normal distribution is a continuous probability distribution with possible values all the reals. Some properties of this distribution are:

Is symmetrical and bell shaped no matter the parameters used. Usually if X is a random variable normally distributed we write this like that:

`X \sim N(\mu , \sigma)`

The two parameters are:

`\mu` who represent the mean and is on the center of the distribution

`\sigma` who represent the standard deviation

One particular case is the normal standard distribution denoted by:

`Z \sim N(0,1)`

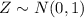
Example: Usually this distribution is used to model almost all the practical things in the life one of the examples is when we can model the scores of a test. Usually the distribution for this variable is normally distributed and we can find quantiles and probabilities associated