Answer:
Therefore the area of rectangle is increased by 15.5%.
Explanation:
Assume the length and width of the rectangle be x and y respectively.
The area of the rectangle is = length×width
=xy.
Now the length of the rectangle is increased by 10%.
Then the length of the rectangle increased =
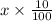 .
.
New length of the rectangle is

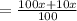
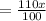
The width of the rectangle is increased by 5%.
Then the width of the rectangle increased =
 .
.
New length of the rectangle is

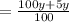

New area of the rectangle is =
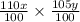
= 1.155 xy.
The percentage of area increase is
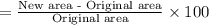
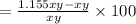
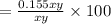
=15.5.
Therefore the area of rectangle is increased by 15.5%.