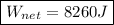Question

How do I go about this?

Answer 1

Hi there!

(a)

Recall that:

`W = F \cdot d = Fdcos\theta`

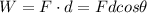
W = Work (J)
F = Force (N)
d = Displacement (m)

Since this is a dot product, we only use the component of force that is IN the direction of the displacement. We can use the horizontal component of the given force to solve for the work.

`W =248(56)cos(30) = 12027.36 J`

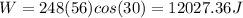
To the nearest multiple of ten:

`W_A = \boxed{12030 J}`

(b)
The object is not being displaced vertically. Since the displacement (horizontal) is perpendicular to the force of gravity (vertical), cos(90°) = 0, and there is NO work done by gravity.

Thus:

`\boxed{W_g = 0 J}`

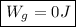
(c)
Similarly, the normal force is perpendicular to the displacement, so:

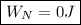
`\boxed{W_N = 0 J}`

(d)

`F_(f) =\mu_k N`

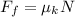
In this instance, the normal force is equivalent to the downward force of gravity and the vertical component of the applied force.

`N = F_g + F_A sin(30)\\\\N = mg + F_A sin(30)\\\\N = 56(9.8) + 248sin(30) = 672.8 N`

Since the force of friction resists the applied force (assigned the positive direction), the work due to friction is NEGATIVE because energy is being LOST. Thus:

`W_f = -\mu_k Nd\\W_f = - (0.1)(672.8)(56) = -3767.68J`

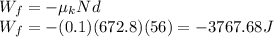
In multiples of ten:

`\boxed{W_f = -3770 J}`

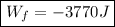
(e)
Simply add up the above values of work to find the net work.

`W_(net) = W_A + W_f \\\\W_(net) = 12027.36 + (-3767.68) = 8259.68 J`

Nearest multiple of ten:

`\boxed{W_(net) = 8260 J}}`

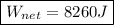
(f)
Similarly, we can use a summation of forces in the HORIZONTAL direction. (cosine of the applied force)

`F_(net) = F_(Ax) - F_f`

`W = F_(net) \cdot d = (F_(Ax) - F_f)`

`W = (F_Acos(30) - \mu_k N)d\\W = (248cos(30) - 0.1(672.8)) * 56 \\\\W = 8259.68 J`

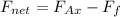
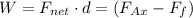
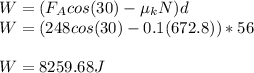
Nearest multiple of ten:

`\boxed{W_(net) = 8260 J}`