Answer:

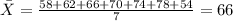


b. 66,8
Explanation:
We have the following data given:
58 , 62 ,66 ,70 , 74 , 78 , 54
Since the data can be modelled with a normal distribution then the best estimator for the true mean is the sample mean given by:

And replacing we got:
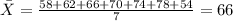
And we can estimate the population deviation with the following formula:

And replacing we got:

And the best solution for this case is:
b. 66,8