Question

In ΔVWX, the measure of ∠X=90°, the measure of ∠W=31°, and XV = 8.4 feet. Find the length of WX to the nearest tenth of a foot.

Answer 1

The length of WX is 14.0 feet.

Explanation:

Consider the right angled triangle VXW below.

According to the trigonometry identities for a right angled triangle the tangent of an angle is the ration of the perpendicular height to the base length.

`tan\ \theta=(P)/(B)`

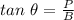
In this case the measure of angle θ is 31°.

The perpendicular is, XV = 8.4 feet.

The base is, WX.

Compute the value of WX as follows:

`tan\ 31^(o)=(XV)/(WX)\\\\0.601=(8.4)/(WX)\\\\WX=(8.4)/(0.601)\\\\WX=13.97671\\\\WX\approx14.0`

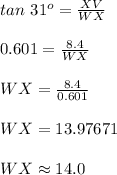
Thus, the length of WX is 14.0 feet.