Answer:
The length of WX is 14.0 feet.
Explanation:
Consider the right angled triangle VXW below.
According to the trigonometry identities for a right angled triangle the tangent of an angle is the ration of the perpendicular height to the base length.
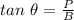
In this case the measure of angle θ is 31°.
The perpendicular is, XV = 8.4 feet.
The base is, WX.
Compute the value of WX as follows:
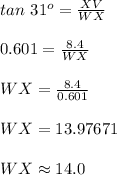
Thus, the length of WX is 14.0 feet.