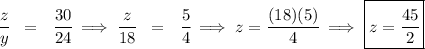Check the picture below.
when running a line, in a right-triangle, from the 90° angle perpendicular to its opposite side, we will end up with three similar triangles, one Small, one Medium and a containing Large one. So let's use proportions to get x,y and z.
![\cfrac{x}{30}~~ = ~~\cfrac{30}{24}\implies \cfrac{x}{30}~~ = ~~\cfrac{5}{4}\implies x=\cfrac{150}{4}\implies \boxed{x=\cfrac{75}{2}} \\\\[-0.35em] ~\dotfill\\\\ \cfrac{y}{24}~~ = ~~\cfrac{x-24}{y}\implies \cfrac{y}{24}~~ = ~~\cfrac{(75)/(2)-24}{y}\implies \cfrac{y}{24}~~ = ~~\cfrac{~~ (27)/(2)~~}{y}\implies \cfrac{y^2}{24}=\cfrac{27}{2} \\\\\\ y^2=\cfrac{(24)(27)}{2}\implies y=\sqrt{\cfrac{(24)(27)}{2}}\implies \boxed{y=18} \\\\[-0.35em] ~\dotfill](https://img.qammunity.org/2023/formulas/mathematics/college/96fifnj849hevznmb45jjm66h85q9pzmm6.png)