Question

A study by Consumer Reports showed that 64% of supermarket shoppers believe supermarket

brands to be as good as national name brands. To investigate whether this result applies
to its own product, the manufacturer of a national name-brand ketchup asked a sample
of shoppers whether they believed that supermarket ketchup was as good as the national
brand ketchup.

a. Formulate the hypotheses that could be used to determine whether the percentage of
supermarket shoppers who believe that the supermarket ketchup was as good as the
national brand ketchup differed from 64%.
b. If a sample of 100 shoppers showed 52 stating that the supermarket brand was as good
as the national brand, what is the p-value?
c. At αα= .05, what is your conclusion?
d. Should the national brand ketchup manufacturer be pleased with this conclusion?
Explain.

Answer 1

(a) Null Hypothesis,
`H_0` : p = 64%

Alternate Hypothesis,
`H_A` : p
`\\eq` 64%

(b) P-value = 0.03632

(c) It is conclude that the percentage of supermarket shoppers who believe that the supermarket ketchup was as good as the national brand ketchup differed from 64%.

(d) No, the national brand ketchup manufacturer would not be pleased with this conclusion.

Explanation:

We are given that a study by Consumer Reports showed that 64% of supermarket shoppers believe supermarket brands to be as good as national name brands.

Let p = percentage of supermarket shoppers who believe that the supermarket ketchup was as good as the national brand ketchup.

(a) Null Hypothesis,
`H_0` : p = 64% {means that the percentage of supermarket shoppers who believe that the supermarket ketchup was as good as the national brand ketchup is equal to 64%}

Alternate Hypothesis,
`H_A` : p
`\\eq` 64% {means that the percentage of supermarket shoppers who believe that the supermarket ketchup was as good as the national brand ketchup differed from 64%}

The test statistics that will be used here is One-sample z proportion statistics;

T.S. =
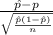`\frac{\hat p-p}{{\sqrt{(\hat p(1-\hat p))/(n) } } } }` ~ N(0,1)

where,
`\hat p` = sample proportion of shoppers stating that the supermarket brand was as good as the national brand =
`(52)/(100)` = 52%

n = sample of shoppers = 100

So, test statistics =
`\frac{0.52-0.64}{{\sqrt{(0.52(1-0.52))/(100) } } } }`

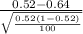
= -2.402

The value of the test statistics is -2.402.

(b) Now, P-value of the test statistics is given by;

P-value = P(Z < -2.402) = 1 - P(Z
`\leq` 2.402)

= 1 - 0.98184 = 0.01816 o

For two-tailed test, P-value =
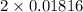`2* 0.01816` = 0.03632 or 3.63%

(c) Since, p-value is less than the level of significance, as 0.03632 < 0.05, so we have sufficient evidence to reject our null hypothesis as it will lie in the rejection region due to which we reject our null hypothesis and conclude that the percentage of supermarket shoppers who believe that the supermarket ketchup was as good as the national brand ketchup differed from 64%.

(d) No, the national brand ketchup manufacturer would not be pleased with this conclusion because he believes that there is no difference between the quality of both the brand ketchup due to which they now have to more focus on their quality to better than other.