Answer:
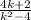 ×
×
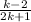 =
=

Explanation:
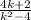 ×
×
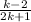
To solve the above, we need to follow the steps below;
4k+2 can be factorize, so that;
4k +2 = 2 (2k + 1)
k² - 4 can also be be expanded, so that;
k² - 4 = (k-2)(k+2)
Lets replace 4k +2 by 2 (2k + 1)
and
k² - 4 by (k-2)(k+2) in the expression given
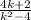 ×
×
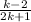
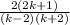 ×
×
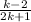
(2k+1) at the numerator will cancel-out (2k+1) at the denominator, also (k-2) at the numerator will cancel-out (k-2) at the denominator,
So our expression becomes;

Therefore,
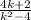 ×
×
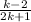 =
=
